Design calculation and verification of 40m high pole wind load

Abstract: High pole lighting range is large, functional, easy to use, in squares, stadiums, overpasses, airports and ports Docks and other applications have a wide range of applications. The safety of high pole lights includes stiffness, stability, economy and many other aspects. Among them, strength calculation and verification are the most important factors. In practical applications, wind loads are affected by high pole lights. The biggest and most critical factor in strength. In this paper, the 40-meter high pole lamp is taken as an example to introduce the design requirements. The design calculation and check of the high-pole lamp wind load are carried out. The calculation results show that the strength of the high pole lamp meets the requirements.

Keywords: safety; wind load; strength calculation; high pole light

Introduction: High pole light means that the pole height is equal to or greater than 20m, as urban roads and highways, High-altitude lighting facilities for large-area lighting such as squares, stadiums, airports, and port terminals. The high pole light is a high-rise structure, so the load design of the high pole light is in line with the load design requirements of the high-rise structure. The loads on the towering structure can be divided into the following three categories.

(1) Permanent load: structural weight, fixed equipment weight, material weight, soil weight, earth pressure, line tension, etc.

( 2) Variable load: wind load, ice load, common earthquake action, snow load, installation and maintenance load, live load on tower floor or platform, temperature change, foundation subsidence, etc.

(3) Accidental load: wire breakage, cable breakage, impact, explosion, rare earthquakes, etc. The snow load is the weight of snow applied to the exposed surface of a building roof or other structure. The snow load value S is determined by the snow weight of the ground area, ie the basic snow pressure So, multiplied by the snow distribution coefficient μr of the house area:

S = μrSo[3]

Basic snow pressure generally refers to specifications or local meteorological records. The specification gives the basic snow pressure in some large and medium-sized cities in China in 10, 50 and 100 years. The general structure takes 50 years of basic snow pressure, temporary buildings, storage, unimportant structures, etc., which can be valued in 10 years and 30 years, or adjusted appropriately. The main factors affecting the snow load of the structure are the snow weight of the local area and the snow distribution on the structural parts. They are directly related to the value of snow load and structural safety. Wrapped ice loads refer to the weight of icing that surrounds the tower bars, cables, and wires. In winter or early spring, under certain climatic conditions, in some areas it is formed by freezing rain, freezing rain, fog, cloud or snow melting below 0 °C, and its value can be determined according to the thickness of the ice and the weight of the ice.

       Wrapbing load is often an important load for structures such as transmission towers and lines. As the ice coating increases the cross section of the rod, the cable, or closes the gap of certain lattices, not only the weight of the structure or the member is increased, but also the wind load is significantly increased due to the increase of the structural wind shield area. It is more unfavorable to force the structure. The damage of seismic loads to high-rise structures is very serious, and the damage often hides the potential danger.

The earthquake theory mainly includes the following three.

(1) Static theory. The theory does not consider the dynamic characteristics of the building. It is assumed that the structure is absolutely rigid. The building motion is absolutely consistent with the ground motion during the earthquake. The maximum acceleration of the building is equal to the maximum acceleration of the ground motion. The maximum load of the building is equal to its mass. The product of the maximum acceleration of the ground. This theory is only applicable to low-rise, rigid buildings.

( 2) Response spectrum theory. It considers the dynamic characteristics of the ground during the earthquake and the dynamic characteristics of the structure itself. It is one of the most widely used seismic design methods in engineering design. The response spectrum theory is a method for analyzing structural reactions based on the reaction of a single particle system under actual earthquakes. In seismic design, the maximum load value under earthquake is usually required. The value is:

F = < span="" style=";font-size:14px;font-family:E-BX;color:rgb(0,0,0)">mamax = w ( g ) amax [3], w is the mass of the mass, which is called the horizontal earthquake influencing factor.

(3) Direct dynamic analysis theory. When the response spectrum is analyzed for large-span flexible structures, the calculation error of the response spectrum method is large due to the influence of nonlinear factors. Direct dynamic analysis theory can overcome the shortcomings of response spectrum theory. The displacement, velocity and acceleration of the structural nodes at various moments during the earthquake can be directly obtained, so as to calculate the vertical

seismic action and the seismic internal forces of the components at various moments. These theories are called direct dynamic analysis theory.

        Temperature effects should consider factors such as temperature changes, solar radiation, and the use of heat sources. The temperature effect acting on the structure or component should be expressed by the change in temperature. When calculating the temperature effect of a structure or component, the linear thermal expansion coefficient of the material should be used. For large or very large structural members composed of different material parts, the temperature effect between the materials of different parts and the temperature field of the whole structural part should be considered.

As one of the structural variable loads, the temperature effect should be considered in combination with other

variable loads depending on the conditions that may occur simultaneously during construction and use.

Because in practical applications, wind load is the biggest and most critical factor affecting the strength of high pole lights. Therefore, we take a 40m high pole lamp as an example to carry out wind loads on high pole lights. Design calculations.

1 Design Requirements

The overall situation of the high pole lights is as follows: The lamp panel is a regular hexagon, the maximum margin of the panel (plus lamps) D = 4170mm, maximum height H = 473mm. On the lamp panel, 18 sets of NESO 4 high-pressure sodium lamps produced by a 1000W company were installed. The weight of the lamps was 34kg and the weight of the lamps was 400kg. See Figure 1.

integrated light The rod is a regular 12-sided shape and is divided into four sections with lengths of 10222mm, 10500mm, 9500mm, and 9500mm. The light pole material is Q345, and the wall thickness is 6mm, 8mm, 8mm and 10mm. The top of the pole is 320mm on the opposite side, and the bottom of the pole is 745mm on the opposite side. The thickness of the lamp post flange is 30mm, the diameter of the inner hole is 771mm, the outer diameter of the flange is 1070mm, and 12 bolt holes with a diameter of 56mm are evenly distributed on the flange. The diameter of the center of the hole is 870mm.

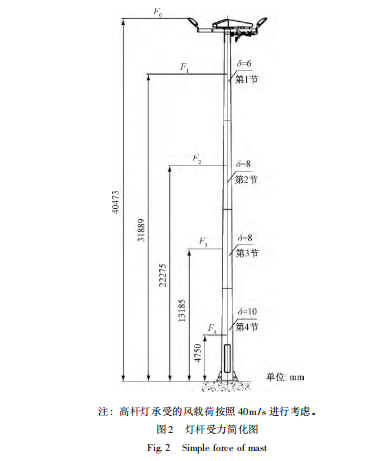
2 High pole light load calculation The wind load of the high pole light is different at different heights, so for the sake of simplicity, we can view each section of the high pole light

is a mass unit divided into five mass units. By calculating the wind load for these mass units (ie, calculating F0, F1, F2,

F3, F4), the wind load of the entire high pole light can be approximated. 126 Journal of Lighting Engineering October 2014

Note: The wind load on a high pole light is considered at 40 m / s.

Fig. 3 Dimensional diagram of high pole light

Fig. 3 Dimemtions of mast The wind load per unit area on the high pole lamp should be as follows Calculation:

ωh = βzμsμzμrωo[2] (1)

where ωh is the wind load per unit area of the high pole lamp (unit: kN /m2); Ωo is the basic wind pressure (unit: kN / m2); μr is the adjustment factor of the return period, 1. 1 for the general high-rise structure, 1. 2 for the important high-rise structure; μz is the wind pressure height at the height of z The coefficient of variation; μs is the wind load body shape coefficient, and the high pole lamp is selected to be 0.7. βz is the wind vibration coefficient at the height of z.

2. 1 Basic wind pressure ωo

The basic wind pressure is calculated as: ωo = V201600[1]

(2) where V0 is Design wind speed (unit: m / s). Substituting the known wind speed of 40 m/s into the above equation, the basic wind pressure is calculated as ωo = 1 kN / m2.

2. 2 The variation coefficient of wind pressure height at different heights is shown in Table 1.

Table 1 Wind pressure height variation coefficient μz

Table 1 Height variation factor of Wind pressure μz from the ground or sea level / m ground roughness category

ABC

5 1. 17 0. 80 0. 54

10 1. 38 1. 00 0. 71

15 1. 52 1. 14 0. 84

20 1. 63 2. 25 0. 94

30 1. 80 1. 42 1. 11

40 1. 92 1. 56 1. 24

50 2. 03 1. 67 1. 36

60 2. 12 1. 77 1. 46 p>

2. 3 Wind vibration coefficient

Because buildings with a height of more than 30 meters belong to high-rise buildings, the wind vibration coefficients of different levels of the same high-rise building are different. The wind vibration coefficient βz of the self-supporting high-rise structure at the Z height can be determined by the following formula:

: βz = 1 + ξε1ε2[1] (3)

where ξ is pulsating Increase the coefficient; ε1 is the influence coefficient of wind pressure pulsation and wind pressure height change; ε2 is the influence coefficient of vibration and structural shape.

ξ, ε1 ε2 See Table 2 to Table 4.

Substituting the wind-induced vibration coefficients in the above table into equation (3), respectively calculate the wind-induced vibration coefficients of the five mass units F0, F1, F2, F3, and F4:

Table 2 Pulsation increase factor

Structural category steel reinforced concrete structure

0. 01 1. 47 1. 11

0. 05 1. 73 1. 18

0. 10 1. 88 1. 23

0. 20 2. 04 1. 28

0. 40 2. 24 1. 34

0. 60 2. 36 1. 38

0. 80 2. 46 1. 42

1. 00 2. 53 1. 44

2. 00 2. 80 1. 54

4. 00 3. 09 1. 65

6. 00 3. 28 1. 72

8. 00 3. 42 1. 77

10. 00 3. 54 1. 82

20. 00 3. 91 1. 96

30. 00 4. 14 2. 06

Note: For H≥ For the 200m reinforced concrete cylinder, the value of the pulsation increase coefficient of the above table can be multiplied by 1.1.

Table 3 Influence coefficient of wind pressure pulsation and wind pressure height change ε1

Table 3 Influence coefficient of wind pressure pulsationand wind pressure height variation ε1

Total height H/m Ground Roughness Category

ABC

10 0. 57 0. 72 0 93

20 0. 51 0. 63 0. 79

40 0. 45 0. 55 0. 69

60 0. 42 0. 50 0. 59

80 0. 39 0. 45 0. 54

100 0. 37 0. 43 0. 50

150 0. 33 0. 37 0. 43

200 0. 30 0. 34 0. 38

250 0. 27 0. 31 0. 34

300 0. 25 0. 28 0. 29

< p="" style="text-align: center;">Table 4 Influence coefficient of vibration mode and structural shape ε2

Table 4 Influence factor for mode, structure and shape Ε2

relative height h /H structure top and bottom width ratio

1. 0 0. 5 0. 3 0. 2 0. 1

1. 0 1. 00 0. 88 0. 76 0. 66 0. 56

0. 9 0. 89 0. 83 0. 73 ( 0. 79) 0. 65 ( 0. 76) 0. 57 ( 0. 84)

0. 8 0. 78 0. 76 0. 67 ( 0. 77) 0. 61 ( 0. 78) 0. 57 ( 0. 96)

0. 7 0. 66 0. 66 0. 60 ( 0. 70) 0. 55 ( 0. 73) 0. 54 ( 0. 94)

0. 6 0. 54 0. 56 0. 51 ( 0. 60) 0. 48 ( 0. 64) 0. 49 ( 0. 84)

0. 5 0. 42 0. 44 0. 41 ( 0. 48) 0. 40 ( 0. 58) 0. 42 ( 0. 69)

0. 4 0. 31 0. 32 0. 31 ( 0. 35) 0. 30 ( 0. 38) 0. 34 ( 0. 52)

0. 3 0. 20 0. 22 0. 22 0. 21 ( 0. 25) 0. 27 ( 0. 38)

0. 2 0. 11 0. 11 0. 12 0. 13 0. 15( 0. 19)

0. 1 0. 04 0. 04 0. 04 0 05 0. 06

Note: Table Brackets, the values in parentheses apply to structural changes linearly; comprises

values outside the suitable number of the recess-shaped structure changes. The remaining values without parentheses are both

.

βz0 = 1 + ξε1ε2 = 1 + 2. 53 × 0. 45 × 0. 88 = 2

βz1 = 1 + ξε1ε2 = 1 + 2. 53 × 0. 45 × 0. 76 = 1. 89

βz2 = 1 + ξε1ε2 = 1 + 2. 53 × 0. 45 × 0. 56 = 1. 64

βz3 = 1 + ξε1ε2 = 1 + 2. 53 × 0. 45 × 0. 32 = 1. 36

βz4 = 1 + ξε1ε2 = 1 + 2. 53 × 0. 45 × 0. 04 = 1. 05 p>

2. 4 Wind load per unit area of each mass unit

The wind pressure height variation coefficient of basic wind pressure, return period adjustment coefficient, and different heights

Wind force coefficient of wind load and wind vibration coefficient at different heights

are substituted into equation (1), respectively, and the wind load per unit area of each

mass unit can be calculated as:

ωh0 = βz0μsμz0μrωo = 2 × 0. 7 × 1. 92 × 1. 2 × 1

= 3. 23 ( kN /m2)

ωh1 = βz1μsμz1μrωo = 1. 89 × 0. 7 × 1. 80 × 1. 2 × 1

= 2. 86 ( kN /m2)

ωh2 = βz2μsμz2μrωo = 1. 64 × 0. 7 × 1. 63 × 1. 2 × 1

= 2. 25 ( kN /m2)

ωh3 = βz3μsμz3μrωo = 1. 36 × 0. 7 × 1 . 52 × 1. 2 × 1

= 1. 74 ( kN /m2)

ωh4 = βz4μsμz4μrωo = 1. 05 × 0. 7 × 1. 17 × 1. 2 × 1

= 1. 03 ( kN /m2)

2. 5 Wind load force of each mass unit F

The wind load force of each mass unit is the single

bit area of the mass unit multiplied by the mass unit area. See the following formula:

F = ωhi × Si

[1] (4)

where Si is the windward area.

F0 = ωh0 × S0 = 3. 23 × 4. 17 × 0. 473 × 0. 8

= 6. 37 ( kN)

Note : Because there are many lamps installed in the lamp panel, consider the

leakage factor of the lamp panel is 0.2, so the actual wind receiving area is the maximum wind surface

product . 8 times.

F1 = ωh1 × S1 = 2. 86 × 10. 222 = 11. 14 ( kN)

F2 = ωh2 × S2 = 2. 25 × 9. 753 = 10. 81 ( kN)

F3 = ωh3 × S3 = 1. 74 × 8. 59 = 8. 86 ( kN)

F4 = ωh4 × S4 = 1. 03 × 8. 435 = 6. 03 ( kN)

2. 6 The bending moment of the roots of each pole of the high pole lamp M

M1 = F0 (0. 473 + 10. 222) + F1 (

10. 2222)

= 68. 11 + 56. 94 = 125. 05 ( kNm)

M2 = F0 ( 0. 473 + 10. 222 + 10. 5 - 0. 747) + F1

(10. 2222 + 10. 5 - 0. 747) + F210. 52= 130. 25 + 165. 58 + 56. 75 = 352. 58 ( kNm)

128 Journal of Lighting Engineering October 2014

M3 = F0 (40. 473 - 9. 5

+ 1. 065) + F1 ( 31. 889 - 9. 5 + 1. 065)

+ F2 ( 13. 185 - 9. 5 + 1. 065) + F3

9. 5 ( 2 )= 204. 08 + 261. 27 + 51. 34 + 42. 09= 558. 78 ( kNm)

M4 = F0 ( 40. 473) + F1 ( 31. 889)+ F2 ( 22. 275) + F3 ( 13. 185)

+ F4 ( 4. 75) = 257. 81 + 355. 24 + 240. 79+ 116. 82 + 28. 64 = 999. 3 ( kNm)

2. 7 Stress calculation at the root of each pole of the pole

stress gauge at the root of each section The formula is:

Fg = MWg

Wg = π( D4 - d4)32D

where: Fg is the stress at the root of each segment of the lamp post; M is the bending moment at the root of each pole of the pole; Wg is the bending section coefficient at the root of each pole of the pole

(here, to simplify the calculation, the pole will be high) The cross section of the lamp is simply

according to the circle; D is the outer diameter of the pole at the root of each segment (take the margin); d is the lamp at the root of each segment

Rod outer diameter (take the edge margin minus the wall thickness).

Wg1 = π( 0. 4424 - 0. 4304)32 × 0. 442 = 0. 88 × 10 - 3 ( m3)

Fg1 = M1Wg1= 125. 05 × 103

0. 88 × 10 - 3 = 142. 1 × 106 ( N /m2)

Wg2 = π( 0. 5434 - 0. 5274)

< p="">32 × 0. 543 = 1. 77 × 10 - 3 ( m3)

Fg2 = M2Wg2= 352. 58 × 103

1. 77 × 10 - 3 = 199 2 × 106 ( N /m2)

Wg3 = π( 0. 6424 - 0. 6264)

32 × 0. 642 = 2. 49 × 10 - 3 ( m3 )

Fg3 = M3Wg3= 558. 78 × 103

2. 49 × 10 - 3 = 224. 4 × 106 ( N /m2) Wg3 = π( 0. 7454 - 0. 7254)32 × 0. 745 = 4. 19 × 10 - 3 ( m3)

Fg4 = M4Wg4= 999. 3 × 103

4. 19 × 10 - 3 = 238. 5 × 106 ( N / m2) Check the "Mechanical Design Manual" to know that the bending resistance of Q345 steel is

, and the service strength value Fg is 345MP (ie 345 × 106N / m2) [4].

Comparing the root stress of each pole of the pole with the yield strength of Q345 material, the stress intensity at each root is less than the yield strength of the material, ie: Fg1 < fg="" ;="" fg2="">< fg="" ;="" fg3="">< fg="" ;="" fg4="">< fg.="" therefore,="" the="" strength="" of="" the="" high="" pole="" lamp="" meets="" the="" requirements.="">

3 Conclusion.

The safety requirements of high poles are particularly high due to the particularity of the range and location of the high pole lighting. When calculating the high pole light intensity, since wind load is the biggest influencing factor, it is important to calculate and check the wind load of the high pole light.

References

[1] Ministry of Construction of the People's Republic of China. High-rise structure design specification GBJ135-90. Beijing: China Building Industry Press, 1991.

[2] Building structure load specification GBJ 9-87. Beijing: Ministry of Environmental Protection and Environmental Protection of the People's Republic of China, 1988.

[3] Steel pole structure design of high pole light. Beijing: Beijing Municipal Design and Research Institute, 1998.

[4] Cheng Daxian. Mechanical design manual. Third Edition, Volume 1. Beijing: Chemical Industry Press, 2011.